Una combinación, es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una combinación nos interesa formar grupos y el contenido de los mismos.
Una combinación es un arreglo donde el orden NO es importante. La notación para las combinaciones es C(n,r) que es la cantidad de combinaciones de “n” elementos seleccionados, “r” a la vez. Es igual a la cantidad de permutaciones de “n” elementos tomados “r” a la vez dividido por “r” factorial. Esto sería P(n,r)/r! en notación matemática.
Determina el número de subgrupos de 1, 2, 3, etc. elementos que se pueden formar con los "n" elementos de una nuestra. Cada subgrupo se diferencia del resto en los elementos que lo componen, sin que influya el orden.
- Por ejemplo, calcular las posibles combinaciones de 2 elementos que se pueden formar con los números 1, 2 y 3.
- Ejemplo: Si se seleccionan cinco cartas de un grupo de nueve, ¿cuantas combinaciones de cinco cartas habría?
La cantidad de combinaciones posibles sería: P(9,5)/5! = (9*8*7*6*5)/(5*4*3*2*1) = 126 combinaciones posibles.
La fórmula para determinar el número de combinaciones es:
nCr = Combinaciones de r objetos tomados de entre n objetos
Donde se observa que,
La expresión anterior nos explica como las combinaciones de r objetos tomados de entre n objetos pueden ser obtenidas a partir de las permutaciones de r objetos tomados de entre n objetos, esto se debe a que como en las combinaciones no nos importa el orden de los objetos, entonces si tenemos las permutaciones de esos objetos al dividirlas entre r!, les estamos quitando el orden y por tanto transformándolas en combinaciones, de otra forma, también si deseamos calcular permutaciones y tenemos las combinaciones, simplemente con multiplicar estas por el r! obtendremos las permutaciones requeridas.
nPr = nCr r!
Y si deseamos r = n entonces;
nCn = n! / (n –n)!n! = n! / 0!n! = 1
¿Qué nos indica lo anterior?
Que cuando se desea formar grupos con la misma cantidad de elementos con que se cuenta solo es posible formar un grupo.
Ejemplos:
1) 1) a. Si se cuenta con 14 alumnos que desean colaborar en una campaña pro limpieza del Tec, cuantos grupos de limpieza podrán formarse si se desea que consten de 5 alumnos cada uno de ellos, b.si entre los 14 alumnos hay 8 mujeres, ¿cuantos de los grupos de limpieza tendrán a 3 mujeres?, c.¿cuántos de los grupos de limpieza contarán con 4 hombres por lo menos?
Solución:
a. n = 14, r = 5
14C5 = 14! / (14 – 5 )!5! = 14! / 9!5!
= 14 x 13 x 12 x 11 x 10 x 9!/ 9!5!
= 2002 grupos
COMBINACIONES CON REPETICION:
¿Qué son? Combinaciones con repetición de m elementos tomados de n en n son los distintos grupos de n elementos iguales o distintos que se pueden hacer con los m elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por CRm,n.
¿Cómo se forman?. Para construir las combinaciones con repetición, partimos del conjunto A={1,2,3,4} y vamos a construir todas las combinaciones con repetición posibles.
De un elemento. Si tenemos un conjunto de cuatro elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos: 1 , 2 , 3 , 4.
De dos elementos. La forma de construirlas será similar a las combinaciones sin repetición aunque con la diferencia de que al permitirse repetir los elementos tendremos que añadir a cada una de las de orden uno, el mismo elemento y todos los siguientes. Así se obtienen: 11 , 12 , 13 , 14 , 22 , 23, 24 , 33 , 34 , 44.
De tres elementos. Se pueden construir a partir de las anteriores añadiendo a cada combinación de orden dos el último elemento y todos los elementos siguientes. Se obtienen: 111 , 112 , 113 , 114 , 122 , 123 , 124 , 133 , 134 , 144 , 222 , 223 , 224 , 233 , 234 , 244 , 333 , 334 , 344 , 444.
De cuatro elementos. Se pueden obtener a partir de las de orden tres, añadiendo a cada una de ellas el último elemento y los elementos siguientes.
De cinco o más elementos. Como estamos construyendo combinaciones con repetición y los elementos se pueden repetir, podríamos continuar construyendo combinaciones de orden cinco o más elementos.
COMBINACIONES SIN REPETICION:
¿Qué son? Combinaciones sin repetición o combinaciones ordinarias de m elementos tomados de n en n (de orden n) son los distintos grupos de n elementos distintos que se pueden hacer con los m elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por Cm,n. (n≤m).
¿Cómo se forman?. Para construir las combinaciones sin repetición, partimos del conjunto A={1,2,3,4} y vamos a construir todas las combinaciones sin repetición posibles.
De un elemento. Si tenemos un conjunto de cuatro elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos: 1 , 2 , 3 , 4.
De dos elementos. A diferencia de las variaciones, si ahora cambiamos de orden los elementos de un grupo, se obtiene el mismo grupo, por lo que para añadir el segundo elemento sólo podremos añadir todos los elementos posteriores y no los anteriores. Así se obtienen: 12 , 13 , 14 , 23, 24 , 34.
De tres elementos. Se pueden construir a partir de las anteriores añadiendo a cada combinación de orden dos los elementos posteriores al segundo. Se obtienen: 123 , 124 , 134 , 234.
De cuatro elementos. Se pueden obtener a partir de las de orden tres, añadiendo a cada una de ellas los elementos posteriores al tercer elemento. Se obtienen: 1234.
Como estamos construyendo combinaciones sin repetición y los elementos no se pueden repetir, ya no podemos continuar construyendo variaciones de orden cinco.
EN ESTE SIGUIENTE VIDEO NOS EXPLICA LA FORMA DE COMO ENCONTRAR LAS COMBINACIONES EN UN PROBLEMA:
Ademas de este video le mostramos unas paginas interactivas donde tendran la oportunidad de poner en practica ejercicios que se le plantean:
http://www.aaamatematicas.com/sta-combin.htm
Estos unos videos donde podran aprender de una forma interactiva la aplicacion de las Combinaciones y Permutaciones:
http://vimeo.com/12160584
http://videos.orange.es/video/iLyROoafMhcy.html
http://videos.orange.es/video/iLyROoafMECi.html
http://www.youtube.com/watch?v=pLuXILeV2dY&feature=channel
http://www.youtube.com/watch?v=GpFX83lTihU&feature=related


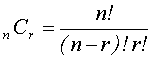

No hay comentarios:
Publicar un comentario